



suivant: Présentation du Problème
monter: Maîtrise d'informatique Université Pierre
précédent: Table des matières
Table des matières
- échanges de données entre programmes
- Transit des données dans des buffers
- Exemple d'un graphe de Kahn[1]
- Contraintes de séquentialité
- Contraintes de buffers vides
- Rappel du Graphe de Kahn[1]
- Contraintes de buffers pleins
- Circuit à l'origine d'un inter-blocage
- Liaisons entre opérations
- Références entre les classes
- Images par
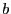 d'un ensemble d'opérations
d'un ensemble d'opérations 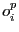
- Images par
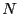 d'un ensemble d'opérations
d'un ensemble d'opérations 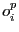
- Transformations successives du problème sur les buffers vers un problème de flots
- Circuit type
- Inter-blocage vide/vide
- Inter-blocage plein/vide
- Déblocage plein/vide
- Inter-blocage plein/plein
- Première façon de débloquer
- Deuxième façon de débloquer
- Exemple
- Graphe de Kahn[1] de l'exemple
- Calcul de
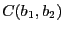
- Calcul de
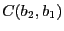
- Calcul de
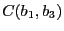 avec
avec
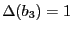
- Calcul de
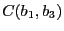 avec
avec
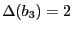
- Calcul de
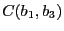 avec
avec
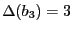
- Calcul de
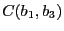 avec
avec
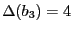
- Calcul de
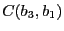 avec
avec
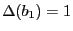
- Calcul de
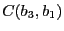 avec
avec
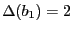
- Calcul de
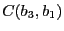 avec
avec
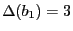
- Calcul de
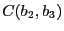 avec
avec
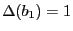
- Calcul de
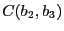 avec
avec
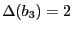
- Calcul de
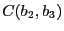 avec
avec
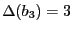
- Calcul de
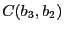 avec
avec
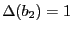
- Calcul de
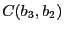 avec
avec
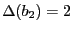
- Instance du problème de la couverture de poids minimal d'un graphe biparti
- Graphe partiel associé à
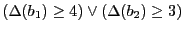
- Problème de flot
Alexandre
2009-05-14