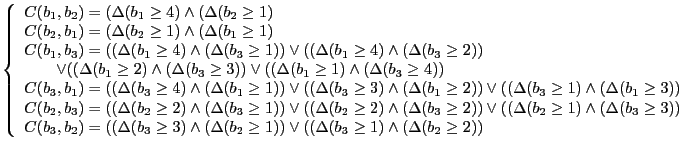![\includegraphics[scale=0.7, clip]{figures/circuit_example/instance.eps}](img196.png)
|
Considérons l'exemple suivant de la figure 3.9. Les buffers sont disposés conformément à la disposition présentée dans le graphe de Kahn[1] de la figure 3.10.
La figure 3.11 explicite le calcul de
![]() ,
les contraintes de buffer vide de
,
les contraintes de buffer vide de ![]() sont tracées et on incrémente progressivement
la capacité de
sont tracées et on incrémente progressivement
la capacité de ![]() jusqu'à ce qu'il n'y ait plus de circuits.
On obtient finalement :
jusqu'à ce qu'il n'y ait plus de circuits.
On obtient finalement :
En faisant de même en permutant les rôles des deux buffers (figure 3.12),
on obtient l'expression
Nous allons procéder de façon analogue pour
![]() , mais en fixant
, mais en fixant
![]() à
à ![]() . La figure 3.13 nous
montre qu'il faut dans ce cas
fixer
. La figure 3.13 nous
montre qu'il faut dans ce cas
fixer ![]() à une valeur supérieure ou égale à
à une valeur supérieure ou égale à ![]() .
.
Les figures 3.13, 3.14, 3.15 et
3.16 nous montrent que :
On déduit des figures 3.17, 3.18 et 3.19
que :
De même les figures 3.20, 3.21 et 3.22
nous montrent que :
Et enfin :
Les conditions nécessaires et suffisantes de non-blocage associées à cet exemple sont donc :