



suivant: Mise sous forme clausale
monter: Présentation d'un algorithme polynomial
précédent: Exemple
Table des matières
A la suite de la première étape, nous nous trouvons avec deux suites d'expressions de la forme citée
précédemment, à savoir
Le graphe est sans circuits si et seulement si, quels que soient 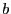 et
et 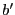 tels
que
tels
que
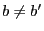 ,
,
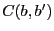 est vrai[2].
Il convient, pour obtenir une solution réalisable, de trouver une interprétation de
l'application
est vrai[2].
Il convient, pour obtenir une solution réalisable, de trouver une interprétation de
l'application 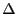 satisfaisant toutes les expressions.
Remarquons au passage que les expressions de type
satisfaisant toutes les expressions.
Remarquons au passage que les expressions de type 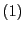 sont un cas particulier des expressions du type
sont un cas particulier des expressions du type 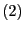 , c'est-à-dire
, c'est-à-dire
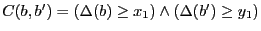 où
où 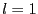 .
.
Sous-sections
Alexandre
2009-05-14