



suivant: Exemple
monter: Conditions nécessaires et suffisantes
précédent: Mise sous forme clausale
Table des matières
Comme nous sommes dans un problème de minimisation, il est possible de définir des restrictions sur les valeurs que
peuvent prendre chaque variable. Par exemple, un intervalle ![$[3; 7]$](img233.png) peut se réduire
à un ensemble de valeurs
peut se réduire
à un ensemble de valeurs
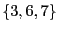 . Nous allons commencer par
les extremums pouvant être pris par
. Nous allons commencer par
les extremums pouvant être pris par 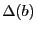 . Tout d'abord, nous définissons :
. Tout d'abord, nous définissons :
En utilisant ces notations, on désigne de même les extremums :
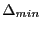 correspond au plus petites valeurs acceptées par toutes les clauses et
correspond au plus petites valeurs acceptées par toutes les clauses et
 est la plus grande valeur trouvée dans toutes les clauses.
Une fois cela fait, on définit pour chaque buffer
est la plus grande valeur trouvée dans toutes les clauses.
Une fois cela fait, on définit pour chaque buffer
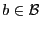 , les
valeurs potentielles
, les
valeurs potentielles
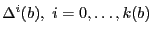 de
la façon suivante :
de
la façon suivante :
-
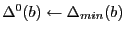 ;
;
-
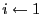 ;
;
- soit
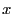 la plus petite valeur telle que
la plus petite valeur telle que
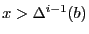 et il existe une expression
contenant l'inégalité
et il existe une expression
contenant l'inégalité
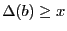 ;
;
- si un tel
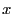 existe :
existe :
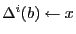 ;
;
-
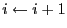 ;
;
- retourner en 3;
- sinon :
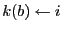 .
.




suivant: Exemple
monter: Conditions nécessaires et suffisantes
précédent: Mise sous forme clausale
Table des matières
Alexandre
2009-05-14
![]() peut se réduire
à un ensemble de valeurs
peut se réduire
à un ensemble de valeurs
![]() . Nous allons commencer par
les extremums pouvant être pris par
. Nous allons commencer par
les extremums pouvant être pris par ![]() . Tout d'abord, nous définissons :
. Tout d'abord, nous définissons :