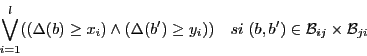Caractérisation des conditions de non-blocage

Cet algorithme calcule des couples de valeurs à partir desquelles on construit un ensemble d'expressions logiques. Il est nécessaire et suffisant de satisfaire toutes ces expressions pour éviter les inter-blocages[2]. Il y a une expression par couple de buffers distincts, on la note $C(b, b^{\prime })$ et elle est de la forme :

$$(\Delta(b)\geq x)\wedge(\Delta(b^{\prime})\geq y)\quad si\ (b, b^{\prime}) \in \mathcal{B}_{ij}^{2}$$

ou bien

$$\bigvee_{i=1}^{l}((\Delta(b)\geq x_{i})\wedge(\Delta(b^{\prim... ...\ (b, b^{\prime}) \in \mathcal{B}_{ij} \times \mathcal{B}_{ji}$$

L'exécution de l'algorithme se fait en deux temps : d'abord pour les couples $(b, b^{\prime}) \in \mathcal{B}_{ij}^{2}$, ensuite pour les couples $(b, b^{\prime}) \in \mathcal{B}_{ij} \times \mathcal{B}_{ji}$.