



suivant: Couples de buffers de
monter: Caractérisation des conditions de
précédent: Détection d'inter-blocages de type
Table des matières
On définit une variable
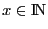 , qui
est la capacité attribuée à
, qui
est la capacité attribuée à 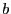 pour tracer ce graphe.
pour tracer ce graphe. 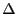 sert ici
à représenter les variables de décision.
sert ici
à représenter les variables de décision.
- initialisations : tracer les contraintes de buffer vide
de
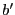 ;
;
-
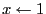 ;
;
- tracer les contraintes de buffer plein de
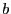 ;
;
- tant qu'il y a des circuits dans la trace d'exécution : ajuster
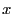 comme décrit dans la section buffer plein/buffer vide;
comme décrit dans la section buffer plein/buffer vide;
- retracer les contraintes de buffer plein de
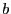 ;
;
- fin de tant que;
-
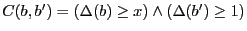 .
.
On peut remarquer que cet algorithme travaille sur deux ensembles d'arcs,
un ensemble fixé par des contraintes de buffer vide,
et un ensemble dont le contenu dépend de la capacité
d'un buffer (conjecturée par la variable 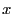 ). Il incrémente la valeur de
). Il incrémente la valeur de 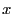 , pour modifier
l'ensemble « variable » d'arcs, jusqu'à ce qu'il n'y
ait plus de circuits.
, pour modifier
l'ensemble « variable » d'arcs, jusqu'à ce qu'il n'y
ait plus de circuits.




suivant: Couples de buffers de
monter: Caractérisation des conditions de
précédent: Détection d'inter-blocages de type
Table des matières
Alexandre
2009-05-14
![]() , qui
est la capacité attribuée à
, qui
est la capacité attribuée à ![]() pour tracer ce graphe.
pour tracer ce graphe. ![]() sert ici
à représenter les variables de décision.
sert ici
à représenter les variables de décision.
![]() ). Il incrémente la valeur de
). Il incrémente la valeur de ![]() , pour modifier
l'ensemble « variable » d'arcs, jusqu'à ce qu'il n'y
ait plus de circuits.
, pour modifier
l'ensemble « variable » d'arcs, jusqu'à ce qu'il n'y
ait plus de circuits.