



suivant: Complexité
monter: Représentations graphiques
précédent: Graphe de Kahn
Table des matières
La trace d'exécution est un graphe orienté dans lequel pour chaque tâche 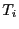 ,
chacune des
,
chacune des 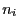 opérations est un sommet. Dans ce graphe figurent trois types d'arcs :
opérations est un sommet. Dans ce graphe figurent trois types d'arcs :
- Contraintes de séquentialité
Une tâche 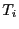 ne peut exécuter
ne peut exécuter 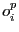 (
(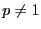 ) que si
) que si 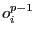 a déjà été exécutée. On notera
a déjà été exécutée. On notera
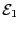 l'ensemble des arcs qui,
pour tout
l'ensemble des arcs qui,
pour tout 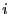 et pour tout
et pour tout 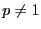 , relie
, relie 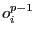 à
à 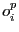 . On remarquera
au passage qu'une variation de la taille des buffers n'influe en rien sur le contenu de
. On remarquera
au passage qu'une variation de la taille des buffers n'influe en rien sur le contenu de
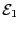 .
.
- Contraintes de buffer vide
Lorsqu'une opération de lecture 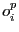 est demandée par
est demandée par 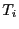 sur un buffer
sur un buffer 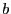 ,
elle ne pourra s'effectuer que si
,
elle ne pourra s'effectuer que si 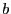 n'est pas vide. Par conséquent, la
n'est pas vide. Par conséquent, la 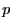 -ème opération de lecture effectuée par une
tâche
-ème opération de lecture effectuée par une
tâche 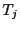 sur le buffer
sur le buffer
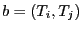 ne pourra être effectuée que si la
ne pourra être effectuée que si la 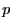 -ème
opération d'écriture de
-ème
opération d'écriture de 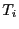 a déjà été effectuée. Nous noterons
a déjà été effectuée. Nous noterons
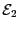 l'ensemble
des arcs qui pour tout buffer
l'ensemble
des arcs qui pour tout buffer
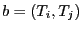 , et pour tout
, et pour tout 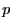 , relie la
, relie la 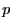 -ème opération
d'écriture sur
-ème opération
d'écriture sur 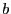 effectuée par
effectuée par 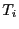 à la
à la 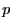 -ème opération de lecture sur
-ème opération de lecture sur 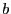 effectuée par
effectuée par 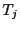 .
Remarquons ici aussi que toute variation des dimensions des buffers laisse l'ensemble
.
Remarquons ici aussi que toute variation des dimensions des buffers laisse l'ensemble
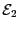 inchangé.
inchangé.
- Contraintes de buffer plein
Lorsqu'une opération d'écriture 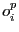 est demandée sur un buffer
est demandée sur un buffer 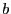 , elle ne pourra s'effectuer que si
, elle ne pourra s'effectuer que si 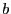 n'est pas plein. Il faut donc attendre qu'une opération de lecture libère un emplacement dans
n'est pas plein. Il faut donc attendre qu'une opération de lecture libère un emplacement dans 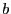 .
Plus formellement, pour qu'une tâche
.
Plus formellement, pour qu'une tâche 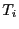 puisse effectuer sa
puisse effectuer sa 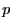 -ème opération d'écriture
sur le buffer
-ème opération d'écriture
sur le buffer
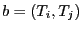 , il faudra avant que
, il faudra avant que 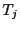 ait effectué sa
ait effectué sa 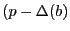 )-ème opération de
lecture sur
)-ème opération de
lecture sur 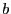 . Nous noterons
. Nous noterons
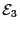 l'ensemble de ces arcs. Remarquons que cette fois-ci, le contenu de
l'ensemble de ces arcs. Remarquons que cette fois-ci, le contenu de
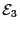 dépend directement des dimensions
dépend directement des dimensions
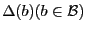 des buffers.
des buffers.
Nous obtenons un graphe
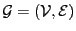 où
où
Par exemple, voici une instance du problème :
Figure 1.4:
Contraintes de séquentialité
|
|
La trace
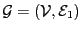 lui correspondant est décrite figure 1.4.
A coté de chaque sommet/opération
lui correspondant est décrite figure 1.4.
A coté de chaque sommet/opération  est indiqué le buffer
est indiqué le buffer 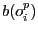 sur lequel elle s'exécute.
Les arcs sont les contraintes de séquentialité des opérations c'est-à-dire sur l'ordre dans
lequel ces dernières doivent s'effectuer. Il suffit donc d'exécuter les opérations
sur lequel elle s'exécute.
Les arcs sont les contraintes de séquentialité des opérations c'est-à-dire sur l'ordre dans
lequel ces dernières doivent s'effectuer. Il suffit donc d'exécuter les opérations 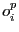 de chaque tâche dans l'ordre induit par
de chaque tâche dans l'ordre induit par 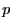 pour respecter ces contraintes.
pour respecter ces contraintes.
Figure 1.5:
Contraintes de buffers vides
|
|
La trace
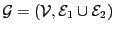 lui correspondant est décrite figure 1.5.
On remarque dans la façon dont sont tracés les arcs qu'à chaque opération de lecture peut
être associée une opération d'écriture. Considérons par exemple l'opération
lui correspondant est décrite figure 1.5.
On remarque dans la façon dont sont tracés les arcs qu'à chaque opération de lecture peut
être associée une opération d'écriture. Considérons par exemple l'opération 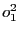 . Comme
. Comme
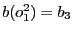 , alors cette opération s'exécute sur un buffer appartenant à
, alors cette opération s'exécute sur un buffer appartenant à
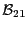 ,
du fait qu'elle est exécutée
par
,
du fait qu'elle est exécutée
par 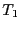 , nous avons affaire à une opération de lecture. Or la lecture d'une donnée dans
un buffer ne peut se faire que si cette donnée
a été préalablement écrite dans ce même buffer. Comme
, nous avons affaire à une opération de lecture. Or la lecture d'une donnée dans
un buffer ne peut se faire que si cette donnée
a été préalablement écrite dans ce même buffer. Comme 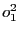 est la première opération de lecture
sur
est la première opération de lecture
sur 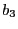 , il faut que la première opération d'écriture sur
, il faut que la première opération d'écriture sur 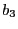 ait été effectuée par
ait été effectuée par 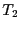 , donc que
, donc que
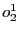 ait déjà été exécutée. D'où la contrainte de précédence
liant
ait déjà été exécutée. D'où la contrainte de précédence
liant 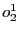 à
à 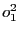 .
.
Figure 1.6:
Rappel du Graphe de Kahn[1]
|
|
Figure 1.7:
Contraintes de buffers pleins
|
|
En posant
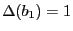 ,
,
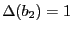 ,
,
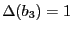 , on obtient la trace
, on obtient la trace
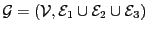 lui correspondant figure 1.7.
Ici sont mentionnées les contraintes dites de buffers pleins. Cela signifie qu'une opération d'écriture dans
un buffer ne pourra être effectuée que si ce buffer n'est pas saturé. Prenons par exemple l'opération
lui correspondant figure 1.7.
Ici sont mentionnées les contraintes dites de buffers pleins. Cela signifie qu'une opération d'écriture dans
un buffer ne pourra être effectuée que si ce buffer n'est pas saturé. Prenons par exemple l'opération
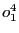 . Comme
. Comme
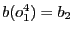 , et que
, et que
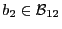 , alors
, alors 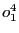 est une opération
d'écriture. Comme
est une opération
d'écriture. Comme
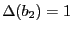 ,
, 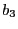 ne peut pas contenir plus d'une donnée à la fois.
Par conséquent,
ne peut pas contenir plus d'une donnée à la fois.
Par conséquent, 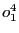 ne pourra être effectuée que lorsque la donnée qui a été écrite dans
ne pourra être effectuée que lorsque la donnée qui a été écrite dans
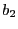 par
par 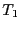 lors de l'exécution de
lors de l'exécution de 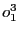 aura été lue. Comme
aura été lue. Comme 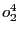 est l'opération de
lecture qui libérera une place dans
est l'opération de
lecture qui libérera une place dans 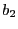 , il faudra que son exécution précède celle de
, il faudra que son exécution précède celle de 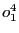 .
C'est pour cette raison qu'il existe un arc
.
C'est pour cette raison qu'il existe un arc
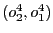
Un circuit dans la trace d'exécution (exemple figure 1.8) correspond à un blocage du système.
Un des algorithmes mis au point pour résoudre ce problème se base sur la recherche de ces circuits.
Figure 1.8:
Circuit à l'origine d'un inter-blocage
|
|




suivant: Complexité
monter: Représentations graphiques
précédent: Graphe de Kahn
Table des matières
Alexandre
2009-05-14
![]() ,
chacune des
,
chacune des ![]() opérations est un sommet. Dans ce graphe figurent trois types d'arcs :
opérations est un sommet. Dans ce graphe figurent trois types d'arcs :
![]() où
où
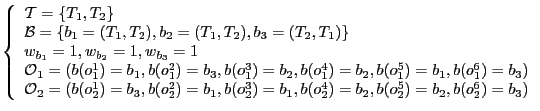
![]() lui correspondant est décrite figure 1.4.
A coté de chaque sommet/opération
lui correspondant est décrite figure 1.4.
A coté de chaque sommet/opération ![]() est indiqué le buffer
est indiqué le buffer ![]() sur lequel elle s'exécute.
Les arcs sont les contraintes de séquentialité des opérations c'est-à-dire sur l'ordre dans
lequel ces dernières doivent s'effectuer. Il suffit donc d'exécuter les opérations
sur lequel elle s'exécute.
Les arcs sont les contraintes de séquentialité des opérations c'est-à-dire sur l'ordre dans
lequel ces dernières doivent s'effectuer. Il suffit donc d'exécuter les opérations ![]() de chaque tâche dans l'ordre induit par
de chaque tâche dans l'ordre induit par ![]() pour respecter ces contraintes.
pour respecter ces contraintes.
![]() ,
,
![]() ,
,
![]() , on obtient la trace
, on obtient la trace
![]() lui correspondant figure 1.7.
Ici sont mentionnées les contraintes dites de buffers pleins. Cela signifie qu'une opération d'écriture dans
un buffer ne pourra être effectuée que si ce buffer n'est pas saturé. Prenons par exemple l'opération
lui correspondant figure 1.7.
Ici sont mentionnées les contraintes dites de buffers pleins. Cela signifie qu'une opération d'écriture dans
un buffer ne pourra être effectuée que si ce buffer n'est pas saturé. Prenons par exemple l'opération
![]() . Comme
. Comme
![]() , et que
, et que
![]() , alors
, alors ![]() est une opération
d'écriture. Comme
est une opération
d'écriture. Comme
![]() ,
, ![]() ne peut pas contenir plus d'une donnée à la fois.
Par conséquent,
ne peut pas contenir plus d'une donnée à la fois.
Par conséquent, ![]() ne pourra être effectuée que lorsque la donnée qui a été écrite dans
ne pourra être effectuée que lorsque la donnée qui a été écrite dans
![]() par
par ![]() lors de l'exécution de
lors de l'exécution de ![]() aura été lue. Comme
aura été lue. Comme ![]() est l'opération de
lecture qui libérera une place dans
est l'opération de
lecture qui libérera une place dans ![]() , il faudra que son exécution précède celle de
, il faudra que son exécution précède celle de ![]() .
C'est pour cette raison qu'il existe un arc
.
C'est pour cette raison qu'il existe un arc
![]()