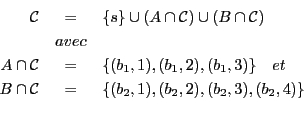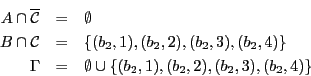suivant: Codes sources
monter: Transformation vers un problème
précédent: Transformation
Table des matières
Figure 3.27:
Problème de flot
|
|
Comme la coupe contient les sommets
Alors
On en déduit que
est une couverture de poids minimal de 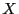 . Les valeurs à
attribuer aux buffers dans ce cas sont :
. Les valeurs à
attribuer aux buffers dans ce cas sont :
Alexandre
2009-05-14
![\includegraphics[scale=0.8, clip]{figures/flots.eps}](img315.png)