



suivant: Exemple
monter: Transformation vers un problème
précédent: Définitions et notations
Table des matières
La transformation se fait comme suit :
Cela signifie que l'on conserve les mêmes sommets, mais :
- que l'on ajoute une source
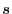 et un puits
et un puits 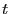 ;
;
- que l'on ajoute des arcs entre
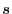 et
et 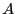 , et entre
, et entre 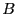 et
et 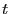 ;
;
- que l'on définit comme capacité sur les arêtes ajoutées
entre
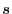 et
et 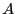 , et entre
, et entre 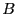 et
et 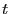 les poids des sommets de
les poids des sommets de
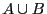 .
.
Un algorithme de flots va définir une coupe
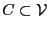 à
partir de laquelle nous allons récupérer la couverture de la façon
suivante : soit
à
partir de laquelle nous allons récupérer la couverture de la façon
suivante : soit 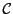 une coupe dans
une coupe dans 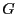 , on a
, on a
On note
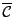 le complémentaire de
le complémentaire de 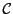 définit ainsi :
définit ainsi :
Une couverture 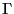 peut se déduire de la coupe de la
façon suivante :
peut se déduire de la coupe de la
façon suivante :
La capacité de la coupe est égale au poids de la
couverture[5].
Par conséquent, trouver la coupe minimale permet de trouver
dans un deuxième temps une couverture de poids minimal.




suivant: Exemple
monter: Transformation vers un problème
précédent: Définitions et notations
Table des matières
Alexandre
2009-05-14
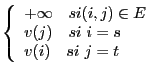
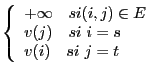
![]() à
partir de laquelle nous allons récupérer la couverture de la façon
suivante : soit
à
partir de laquelle nous allons récupérer la couverture de la façon
suivante : soit ![]() une coupe dans
une coupe dans ![]() , on a
, on a