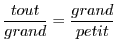
Si l'on observe la figure 2, le nombre d'Or,
noté ![]() , est celui qui permet d'avoir le rapport
, est celui qui permet d'avoir le rapport
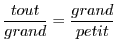
Si la grande partie est de longueur ![]() , on note autrement dit
, on note autrement dit
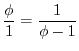 . En résolvant
cette équation (voir l'annexe A), on obtient
. En résolvant
cette équation (voir l'annexe A), on obtient
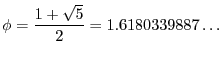 . Ce
nombre est irrationnel (de par la présence de
. Ce
nombre est irrationnel (de par la présence de ![]() ), cela
signifie qu'il est impossible de l'obtenir en divisant deux nombres
entiers. On appelle section d'Or la partie décimale du nombre
d'Or, à savoir
), cela
signifie qu'il est impossible de l'obtenir en divisant deux nombres
entiers. On appelle section d'Or la partie décimale du nombre
d'Or, à savoir
![]() . Une propriété tout à fait
surprenante est que la section d'Or est l'inverse du nombre
d'Or. Autrement dit
. Une propriété tout à fait
surprenante est que la section d'Or est l'inverse du nombre
d'Or. Autrement dit
![]()