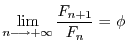 . On le
vérifie après avoir constaté que comme
. On le
vérifie après avoir constaté que comme
On définit de façon formelle la suite de Fibonacci ![]() de la façon
suivante :
de la façon
suivante : ![]() ,
, ![]() et
et
![]() . le terme
général de
. le terme
général de ![]() est donné par
est donné par
![]() (se
prouve aisément par récurrence). Cela explique pourquoi
(se
prouve aisément par récurrence). Cela explique pourquoi
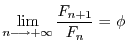 . On le
vérifie après avoir constaté que comme
. On le
vérifie après avoir constaté que comme
![]() , alors
, alors
![]() .
.
|
|
|
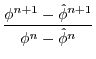 |
| |
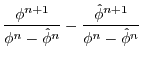 |
|
|
|
|
|
| |
|